การประมวลผลภาพด้วยเครื่องคอมพิวเตอร์ Image processing

ขั้นตอนที่ 1 ขั้นตอนกระบวนการก่อนการประมวลผลภาพ (Pre-processing)

การปรับแก้ภาพมีวัตถุประสงค์เพื่อปรับแก้ความคลาดเคลื่อนของข้อมูล (Data error) สัญญาณที่รบกวน (Noise) และความบิดเบี้ยวเชิงเรขาคณิตที่เกิดขึ้นในระหว่างกระบวนการถ่ายภาพ การบันทึกข้อมูลสัญญาณ การสะท้อนคลื่นแม่เหล็กไฟฟ้า การส่งสัญญาณ และการโคจรของดาวเทียม มีกระบวนการปรับแก้ 2 กระบวนการที่ต้องกระทำ ดังนี้

การตรวจแก้คลื่นรังสี (Radiometric correction)

ก่อนที่จะส่งข้อมูลจากระยะไกลให้กับผู้ใช้งาน ข้อมูลเหล่านี้จะต้องผ่านการตรวจแก้คลื่นรังสีจากสถานีรับสัญญาณดาวเทียมภาคพื้นดินมาแล้วระดับหนึ่ง แต่บางครั้งยังปรากฏข้อบกพร่องทางเชิงคลื่น เนื่องจากสาเหตุหลายประการ เช่น การรบกวนจากชั้นบรรยากาศ หรือจากความบกพร่องของเครื่องรับสัญญาณ ทำให้เกิดความไม่ชัดเจนพร่ามัว มีลายเส้นปะปน (Strip/Noise) ปรากฏบนข้อมูลจากดาวเทียม ปัญหาอีกด้านหนึ่งที่จำเป็นต้องมีการตรวจแก้คลื่นรังสี คือ เมื่อต้องการใช้ข้อมูลหลายช่วงเวลาเพื่อการศึกษาการเปลี่ยนแปลงของปรากฏการณ์ใดปรากฏการณ์หนึ่งต้องทำการปรับแก้ค่ามุมยกของดวงอาทิตย์ (Sun elevation correction) ที่เปลี่ยนแปลงไปตามแต่ละช่วงเวลาและแต่ละฤดูกาล การแก้ไขปัญหาดังกล่าวทำได้โดยการตรวจแก้คลื่นรังสี พร้อมทั้งต้องมีรายละเอียดตัวแปร (Parameters) เกี่ยวกับการรับสัญญาณ มุมที่ดาวเทียมกระทำกับแสงดวงอาทิตย์ (Solar illumination angles) ค่ารังสีตกกระทบ(Irradiance) การกระจายแสงในเส้นทางผ่าน (Path radiance) ค่าการสะท้อนของวัตถุเป้าหมาย (Reflectance of target) ค่าการส่งผ่านของบรรยากาศ เป็นต้น และข้อมูลสภาวะอากาศในขณะที่ทำการบันทึกข้อมูล การปรับแก้มี กรรมวิธีในการคำนวณที่ซับซ้อนมาก โดยต้องใช้ซอฟต์แวร์ที่มีโปรแกรมเฉพาะสำหรับการตรวจแก้คลื่นรังสี ซึ่งโดยทั่วไปการแก้ไขข้อบกพร่องเชิงคลื่นจะต้องทำ ได้แก่

1) การชดเชยค่าการสะท้อนที่บิดเบือนของสภาวะอากาศ (Haze compensation) เกิดขึ้นจากการกระจัดกระจายแสงในบรรยากาศ จึงทำให้เกิดการสลัวของแสง (Haze) ทำให้ภาพมีลักษณะไม่ชัดเจน ไม่คมชัดการแก้ไขทำโดยการลดผลการกระจัดกระจายแสงในบรรยากาศให้น้อยที่สุด โดยการเปรียบเทียบค่าความสว่างทั่วไปกับค่าความสว่างต่ำที่สุด (Zero reflectance) ซึ่งส่วนใหญ่จะเป็นวัตถุที่ดูดกลืนพลังงานมาก เช่น น้ำใสจะมีการดูดกลืนสูงมากในช่วงคลื่นอินฟราเรด

2) การเปลี่ยนค่าความสว่างเป็นค่าการแผ่รังสีสมบูรณ์ (Conversion of digital numbers to absolute radiance value) เป็นการตรวจแก้คลื่นรังสีอีกวิธีหนึ่ง โดยการแปลงค่าความสว่างเป็นค่าการแผ่รังสี คำนวณจากข้อมูลค่าการแผ่รังสีสูงสุด และการแผ่รังสีต่ำสุดในแต่ละช่วงคลื่น ตามสูตรต่อไปนี้

L = [(LMAX – LMIN) / 255] × DN + LMIN

โดยที่         L = ค่าการแผ่รังสีตามช่วงคลื่น (Spectral radiance)

LMAX = ค่าการแผ่รังสีสูงสุด ซึ่งแปลงจากค่าความสว่างสูงสุดในช่วงคลื่นนั้น (DN = 255)

LMIN = ค่าการแผ่รังสีต่ำสุด ซึ่งแปลงจากค่าความสว่างต่ำสุดในช่วงคลื่นนั้น (DN = 0)

DN = ค่าการสะท้อนของจุดภาพ (Digital number)

3) การลบสัญญาณรบกวน (Noise removal) ผลจากความบกพร่องของเครื่องรับสัญญาณมีผลให้เกิดสัญญาณรบกวนในข้อมูลภาพ หรือข้อมูลส่วนนั้นสัญญาณขาดหายไป ปรากฏเป็นลายเส้นแทรกอยู่ในเนื้อภาพหรือเป็นจุดๆ กระจายไปทั่วภาพ (Salt and pepper effect) การแก้ไขทำได้โดยใช้ตัวกรองภาพแบบค่าเฉลี่ยเลขคณิตหรือค่ากึ่งกลางเลขคณิต (Mean or median filters) มาคำนวณค่าเฉลี่ยจากจุดภาพอื่นที่อยู่โดยรอบบริเวณที่สัญญาณหายไป และตัวกรองจำเพาะที่ใช้สำหรับกรองจุดกรองแต่ยังคงรักษาขอบเขตและเนื้อภาพของจุดข้อมูล

การตรวจแก้เชิงเรขาคณิต (Geometric correction)

ก่อนนำข้อมูลจากดาวเทียมไปใช้ประโยชน์มีความจำเป็นต้องปรับแก้เชิงเรขาคณิต เพราะพิกัดตำแหน่งของวัตถุต่างๆ มีความคลาดเคลื่อนไปจากความเป็นจริง เนื่องจากข้อบกพร่องทางเครื่องรับสัญญาณและรูปลักษณะของวัตถุ การตรวจแก้เชิงเรขาคณิตมีความจำเป็นมากยิ่งขึ้น เมื่อต้องการนำข้อมูลจากระยะไกลไปใช้งานร่วมกับข้อมูลเชิงแผนที่อื่นๆ เพื่อให้สามารถซ้อนทับกันได้ หรือหากต้องการศึกษาปรากฏการณ์อย่างหนึ่งในหลายช่วงเวลาการเปรียบเทียบข้อมูลแต่ละช่วงเวลาต้องมีระบบพิกัดเดียวกัน จึงจะสามารถซ้อนข้อมูลแต่ละเวลาลงกันได้สนิทจึงจำเป็นต้องทำการปรับแก้เชิงเรขาคณิต

1) สาเหตุของความบิดเบี้ยวทางเรขาคณิต การบิดเบี้ยวทางเรขาคณิต (Geometric distortion) คือ ความผิดพลาดซึ่งเกิดขึ้นเนื่องจากพิกัดของภาพไม่เป็นไปตามระบบพิกัดแผนที่ ความบิดเบี้ยวเชิงเรขาคณิต มี 2 ลักษณะ คือ

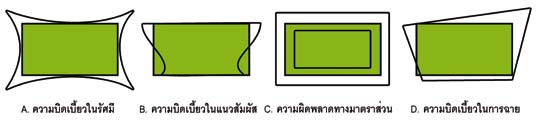
1.1) ความบิดเบี้ยวภายใน (Internal distortion) มีสาเหตุมาจากความบกพร่องของอุปกรณ์ในเครื่องวัดสัญญาณ เช่น ความบิดเบี้ยวในรัศมีของเลนส์ ทำให้บริเวณที่ห่างจากจุดศูนย์กลางภาพมีความบิดเบี้ยวมากขึ้น ความบิดเบี้ยวในแนวสัมผัสของเลนส์ ความผิดพลาดของความยาวโฟกัส การเอียงของระนาบภาพ ความไม่คงที่ของระนาบภาพ ความผิดพลาดในการจัดแนวของแผงรับสำหรับเครื่องวัดแบบแผงเชิงเส้น (Linear array sensor)ความไม่คงที่ของอัตราสุ่มตัวอย่าง ความผิดพลาดของเวลาสุ่มตัวอย่าง ความไม่คงที่ของความเร็วของกระจกกวาด เป็นต้น

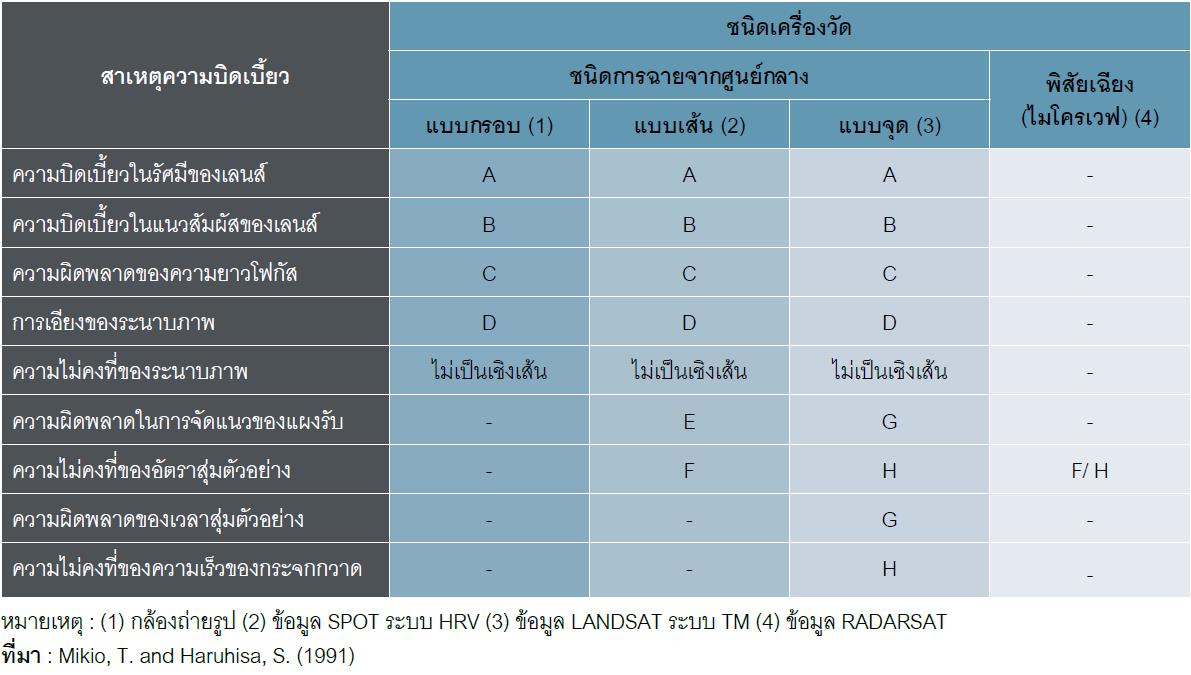
1.2) ความบิดเบี้ยวภายนอก (External distortion) มีสาเหตุหลายประการ เช่น จากการทรงตัวของเครื่องวัด ความไม่คงที่ของการทรงตัว ความโค้งและการเคลื่อนที่ของโลก การหมุนของโลก บรรยากาศและการหักเหของชั้นบรรยากาศ ความผิดพลาดเชิงระนาบของยาน ความผิดพลาดทางระดับความสูงของยาน การเคลื่อนที่ทางตำแหน่งวงโคจร ความโค้งของผิวโลก ความสูงของพื้นผิว และรูปร่างวัตถุ เป็นต้น

2) วิธีการตรวจแก้เชิงเรขาคณิต มีหลักการตรวจแก้โดยการสร้างความสัมพันธ์ของระบบพิกัดระหว่างข้อมูลที่ปรับแก้ (Rectified image) กับระบบพิกัดภูมิศาสตร์ของข้อมูลอ้างอิง (Reference image) เพื่อที่พิกัดของข้อมูลที่ต้องการตรวจแก้ ถูกเปลี่ยนให้เป็นระบบพิกัดใหม่ตามระบบพิกัดของข้อมูลอ้างอิง ข้อมูลอ้างอิงจะเป็นข้อมูลจากระยะไกลเช่นเดียวกันก็ได้ เช่น ในกรณีที่ต้องการศึกษาข้อมูลในพื้นที่เดียวกันแบบหลายช่วงเวลา ในกรณีนี้ เรียกว่า เป็นการตรวจแก้ระหว่างภาพกับภาพ (Image to image correction) หรือข้อมูลอ้างอิงอาจเป็นแผนที่ภูมิประเทศหรือแผนที่เฉพาะที่มีระบบพิกัด หากต้องการนำข้อมูลจากระยะไกลไปศึกษาร่วมกับข้อมูลแผนที่อื่นๆ หรือเพื่อเปรียบเทียบกับสภาพจริงในพื้นที่ศึกษา ในกรณีนี้ เรียกว่า การตรวจแก้ระหว่างภาพกับแผนที่ (Image to map correction) การตรวจแก้เชิงเรขาคณิตมีวิธีการ 3 วิธี ดังต่อไปนี้

2.1) การตรวจแก้แบบมีระบบ (Systematic correction) เป็นการปรับแก้ตามค่าอ้างอิงเชิงเรขาคณิตต่างๆ ที่กำหนดไว้ก่อนแล้ว ทำให้ความผิดพลาดที่เกิดขึ้นสามารถแก้ไขได้อย่างมีระบบ เช่น เรขาคณิตของกล้องถ่ายรูปชนิดเลนส์ จะถูกกำหนดโดยสมการร่วมเชิงเส้นด้วยความยาวโฟกัสที่ปรับเทียบแล้ว การตรวจแก้เชิงสัมผัสผิว (Tangent correction) ของเครื่องกวาดภาพแบบกลเชิงแสง ก็จัดอยู่ในการตรวจแก้แบบมีระบบ โดยทั่วไปการตรวจแก้แบบมีระบบสามารถแก้ไขความผิดพลาดได้ทั้งหมด การคำนวณตรวจแก้เชิงเรขาคณิตสำหรับข้อมูลจากระยะไกล มักจะทำมาแล้วระดับหนึ่งจากสถานีรับ และแปลงสัญญาณ เรียกว่าเป็นระดับ Bulk คือ แก้ไขความบิดเบือนจากสาเหตุทั้งแบบภายในและภายนอกแต่พิกัดข้อมูลยังเป็นระบบพิกัดของแถวและสดมภ์ของข้อมูลภาพ ตามโครงสร้างข้อมูลแบบแรสเตอร์

2.2) การตรวจแก้แบบไม่มีระบบ (Non systematic correction) เป็นการตรวจแก้จากพิกัดของระบบภาพไปสู่ระบบที่มีพิกัด โดยอาศัยสมการพหุนาม (Polynomial equation) วิธีนี้ต้องมีการหาค่าพิกัดจากจุดควบคุมภาคพื้นดิน (Ground Control Point : GCP) ที่รู้ค่าพิกัดจากแผนที่ภูมิประเทศ หรือแผนที่เฉพาะเรื่องที่มีพิกัด หรือจากพิกัดจริง ซึ่งวัดจากดาวเทียมระบบกำหนดตำแหน่งบนโลก จุดควบคุมภาคพื้นดินใช้เป็นข้อมูลในการคำนวณสมการคณิตศาสตร์ เพื่อเปรียบเทียบระหว่างระบบพิกัดภาพและระบบพิกัดภูมิศาสตร์ การคำนวณใช้หลักการวิธีการกำลังสองน้อยที่สุด (Least square method) และสามารถกำหนดระดับความแม่นยำได้จากลำดับการยกกำลัง (Order) ของสมการพหุนาม จำนวน และการกระจายตัวของจุดควบคุมภาคพื้นดิน

2.3) การตรวจแก้แบบวิธีผสม (Combined method) เป็นการปรับแก้โดยนำวิธีการปรับแก้ทั้งสองแบบข้างต้นมาใช้ร่วมกัน ซึ่งเป็นวิธีการปกติที่นิยมทำกันทั่วไปกับข้อมูลจากระยะไกล โดยการตรวจแก้แบบมีระบบจะถูกคำนวณเสมอที่สถานีรับข้อมูลก่อนจะมีการแจกจ่ายข้อมูลไปสู่ผู้ใช้งาน และการตรวจแก้แบบไม่มีระบบเป็นส่วนที่ทำตามมาโดยผู้ใช้งาน เพื่อให้ตรงกับวัตถุประสงค์ในการประยุกต์ใช้ โดยมากยอมรับให้มีความผิดพลาดของการปรับแก้ไม่เกินหนึ่งจุดภาพของตำแหน่งจริงของจุดนั้นๆ ในกรณีของภาพถ่ายดิ่ง

3) การหาจุดควบคุมภาคพื้นดิน การตรวจแก้เชิงเรขาคณิตจะมีความถูกต้องมากหรือน้อยขนาดไหนขึ้นอยู่กับวิธีการเลือกจุดควบคุมภาคพื้นดิน จุดควบคุมภาคพื้นดิน เป็นจุดที่ตำแหน่งใดก็ได้บนข้อมูลจากดาวเทียมและปรากฏได้ชัดเจนเป็นจุดเดียวกันบนข้อมูลอ้างอิง จุดควบคุมภาคพื้นดินที่ดีส่วนใหญ่ต้องเป็นจุดที่มีความคงที่ของรูปทรงโดยเฉพาะในระหว่างเวลาที่มีข้อมูลจากระยะไกลและข้อมูลอ้างอิง ต้องเป็นจุดที่สังเกตได้ง่าย ได้แก่ จุดตัดของวัตถุต่างๆ (เช่น สี่แยกถนนตัดกัน แปลงนา มุมของอาคาร ฯลฯ) จุดที่โดดเด่น (เช่น ต้นไม้ในนาข้าว บ้านกลางนาเกลือ พื้นที่หินโผล่บนภูเขายอดเขา) โดยอาศัยการสังเกตความแตกต่างของค่าความสว่างระหว่างวัตถุที่แตกต่างกันมาประกอบการพิจารณา จุดควบคุมภาคพื้นดินควรมีจำนวนมากพอ และกระจายอย่างสม่ำเสมอทั่วพื้นที่ศึกษา มีมากกี่จุดก็ได้ เพื่อควบคุมการแปลงพิกัดให้เกิดขึ้นอย่างสม่ำเสมอทั่วพื้นที่ ถ้าจุดควบคุมภาคพื้นดินไปรวมกลุ่มอยู่เฉพาะบางบริเวณความถูกต้องบริเวณนั้นจะมีมากกว่าบริเวณที่มีจุดควบคุมภาคพื้นดินน้อยกว่า

4) การคำนวณการตรวจแก้เชิงเรขาคณิต ประกอบด้วยการคำนวณ 2 ขั้นตอน คือ

4.1) การแปลงค่าพิกัด (Geometric coordinate transformation) ระหว่างข้อมูลภาพเริ่มต้น(x¹,y¹) และพิกัดภูมิศาสตร์ (x,y) มีการตรวจแก้เชิงเรขาคณิตโดยใช้สูตรของสมการเชิงเส้นเพื่อหาตำแหน่งพิกัดใหม่กระบวนการนี้ เรียกว่า การประมาณค่าเชิงพื้นที่ (Spatial interpolation) มีสูตรสมการดังนี้

x¹ = a₀ + a₁x + a₂y

y¹ = b₀ + b₁x + b₂y

โดยที่  x¹ = พิกัดของด้านสดมภ์ของข้อมูลนำเข้า (original input image)

y¹ = พิกัดของด้านแถวของข้อมูลภาพนำเข้า

x = พิกัดของด้านสดมภ์ของข้อมูลภาพผลลัพธ์ (output image)

y = พิกัดของด้านแถวของข้อมูลภาพก่อนผลลัพธ์

การตรวจสอบความถูกต้องของการตรวจแก้ คำนวณโดยใช้หลักการถดถอยกำลังสองน้อยที่สุด(Least square regression method) การหาค่าความถูกต้องคำนวณจากรากที่สองของค่าเฉลี่ยของความคลาดเคลื่อนจากแต่ละจุดควบคุมภาคพื้นดิน (Root method) การหาค่าความถูกต้องคำนวณจากรากที่สองของค่าเฉลี่ยของความคลาดเคลื่อนจากแต่ละจุดควบคุมภาคพื้นดิน (root mean square error : RMS_error) มีสูตรคำนวณ ดังนี้

โดยที่  RMS_error = ค่าความถูกต้องของจุดควบคุมภาคพื้นดิน

x_orig, y_orig = ค่าพิกัดของจุดควบคุมภาคพื้นดินในภาพก่อนตรวจแก้

ค่า RMS_error จะบอกได้ว่า จุดควบคุมภาคพื้นดินมีตำแหน่งพิกัดใกล้เคียงกับพิกัดอ้างอิงเพียงใด (มีหน่วยเป็นจุดภาพ) โดยมากยอมรับค่าที่มีค่าบวกหรือลบไม่เกิน 1 จุดภาพ ถ้าค่า RMS_error มีค่าสูง หมายความว่าความคลาดเคลื่อนทางตำแหน่งยังมีมาก สามารถคำนวณเป็นหน่วยเมตริก โดยนำค่า RMS_error คูณกับขนาดของจุดภาพ

4.2) การประมาณค่าของจุดภาพ (interpolation) สิ่งที่ต้องทำหลังจากแปลงค่าพิกัดตำแหน่ง คือ ต้องประมาณค่าของจุดภาพ หรือค่าความสว่างของจุดภาพใหม่ โดยมีการประมาณค่าใหม่ (Intensity interpolation)ซึ่งมีวิธีการคำนวณได้ทั้งหมด 3 วิธี ได้แก่

4.2.1) การประมาณค่าจากตำแหน่งใกล้ที่สุด (Nearest Neighbor interpolation : NN) ค่าความสว่างใหม่จะถูกกำหนดจากค่าความสว่างของจุดภาพในภาพก่อนตรวจแก้ โดยเลือกเอาตำแหน่งที่อยู่ใกล้ที่สุดวิธีการนี้มีข้อดีตรงที่สามารถรักษาค่าความสว่างให้ใกล้เคียงกับภาพก่อนตรวจแก้ได้มากที่สุด หรือแทบจะไม่มีการเปลี่ยนแปลงเลย

4.2.2) การประมาณค่าแบบเส้นคู่ (Bi-Linear interpolation : BL) เป็นการประมาณค่า ความสว่างใหม่โดยคำนวณระยะทางโดยน้ำหนักระหว่าง 4 จุดที่อยู่รอบจุดนั้น ซึ่งจุดภาพที่ใกล้จะให้น้ำหนักมากกว่าจุด ที่อยู่ไกล ดังนี้

โดยที่  BV_wt = ค่าความสว่างใหม่

Z_k = ค่าความสว่างของจุดภาพที่อยู่โดยรอบจุดนั้น

D_k = ระยะห่างของจุดนั้นกับจุดอื่นที่อยู่โดยรอบ

ค่าความสว่างใหม่วิธีนี้จึงทำให้ข้อมูลภาพเกิดความเรียบต่อเนื่อง (Smooth) มีรายละเอียดลดลงจาก

ข้อมูลภาพเริ่มต้น

4.2.3) การประมาณค่าแบบการประสานเชิงลูกบาศก์ (Cubic Convolution interpolation : CC) ค่าความสว่างใหม่จะถูกประมาณด้วยฟังก์ชัน ลูกบาศก์โดยใช้จุดภาพ 16 จุดที่อยู่ล้อมรอบ วิธีการคำนวณแบบนี้ให้ผลที่ดี ทั้งในด้านความคมชัดและการต่อเนื่อง แต่ต้องใช้เวลาคำนวณมากกว่าเมื่อเทียบกับวิธีอื่น และค่าความสว่างใหม่จะเป็นค่าเฉลี่ยจากจุดภาพโดยรอบทั้งหมด ซึ่งอาจแตกต่างจากกับค่าความสว่างเดิมมาก

ที่มา : ตำราเทคโนโลยีอวกาศและภูมิสารสนเทศศาสตร์